Drucker–Prager yield criterion
| Continuum mechanics |
|---|
The Drucker–Prager yield criterion[1] is a pressure-dependent model for determining whether a material has failed or undergone plastic yielding. The criterion was introduced to deal with the plastic deformation of soils. It and its many variants have been applied to rock, concrete, polymers, foams, and other pressure-dependent materials.
The Drucker–Prager yield criterion has the form
where 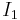 is the first invariant of the Cauchy stress and
is the first invariant of the Cauchy stress and 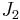 is the second invariant of the deviatoric part of the Cauchy stress. The constants
is the second invariant of the deviatoric part of the Cauchy stress. The constants 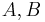 are determined from experiments.
are determined from experiments.
In terms of the equivalent stress (or von Mises stress) and the hydrostatic (or mean) stress, the Drucker–Prager criterion can be expressed as
where 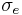 is the equivalent stress,
is the equivalent stress, 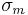 is the hydrostatic stress, and
is the hydrostatic stress, and 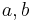 are material constants. The Drucker–Prager yield criterion expressed in Haigh–Westergaard coordinates is
are material constants. The Drucker–Prager yield criterion expressed in Haigh–Westergaard coordinates is
The Drucker–Prager yield surface is a smooth version of the Mohr–Coulomb yield surface.
Contents |
Expressions for A and B
The Drucker–Prager model can be written in terms of the principal stresses as
If 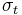 is the yield stress in uniaxial tension, the Drucker–Prager criterion implies
is the yield stress in uniaxial tension, the Drucker–Prager criterion implies
If 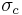 is the yield stress in uniaxial compression, the Drucker–Prager criterion implies
is the yield stress in uniaxial compression, the Drucker–Prager criterion implies
Solving these two equations gives
Uniaxial asymmetry ratio
Different uniaxial yield stresses in tension and in compression are predicted by the Drucker–Prager model. The uniaxial asymmetry ratio for the Drucker–Prager model is
Expressions in terms of cohesion and friction angle
Since the Drucker–Prager yield surface is a smooth version of the Mohr–Coulomb yield surface, it is often expressed in terms of the cohesion ( ) and the angle of internal friction (
) and the angle of internal friction ( ) that are used to describe the Mohr–Coulomb yield surface. If we assume that the Drucker–Prager yield surface circumscribes the Mohr–Coulomb yield surface then the expressions for
) that are used to describe the Mohr–Coulomb yield surface. If we assume that the Drucker–Prager yield surface circumscribes the Mohr–Coulomb yield surface then the expressions for  and
and  are
are
If the Drucker–Prager yield surface inscribes the Mohr–Coulomb yield surface then
-
Derivation of expressions for 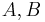 in terms of
in terms of 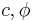
The expression for the Mohr–Coulomb yield criterion in Haigh–Westergaard space is If we assume that the Drucker–Prager yield surface circumscribes the Mohr–Coulomb yield surface such that the two surfaces coincide at
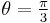 , then at those points the Mohr–Coulomb yield surface can be expressed as
, then at those points the Mohr–Coulomb yield surface can be expressed asor,
The Drucker–Prager yield criterion expressed in Haigh–Westergaard coordinates is
Comparing equations (1.1) and (1.2), we have
These are the expressions for
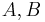 in terms of
in terms of 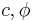 .
.On the other hand if the Drucker–Prager surface inscribes the Mohr–Coulomb surface, then matching the two surfaces at
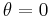 gives
gives
Drucker–Prager model for polymers
The Drucker–Prager model has been used to model polymers such as polyoxymethylene and polypropylene[2]. For polyoxymethylene the yield stress is a linear function of the pressure. However, polypropylene shows a quadratic pressure-dependence of the yield stress.
Drucker–Prager model for foams
For foams, the GAZT model [3] uses
where 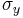 is a critical stress for failure in tension or compression,
is a critical stress for failure in tension or compression,  is the density of the foam, and
is the density of the foam, and 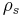 is the density of the base material.
is the density of the base material.
Extensions of the isotropic Drucker–Prager model
The Drucker–Prager criterion can also be expressed in the alternative form
Deshpande–Fleck yield criterion
The Deshpande–Fleck yield criterion[4] for foams has the form given in above equation. The parameters 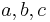 for the Deshpande–Fleck criterion are
for the Deshpande–Fleck criterion are
where  is a parameter[5] that determines the shape of the yield surface, and
is a parameter[5] that determines the shape of the yield surface, and 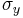 is the yield stress in tension or compression.
is the yield stress in tension or compression.
Anisotropic Drucker–Prager yield criterion
An anisotropic form of the Drucker–Prager yield criterion is the Liu–Huang–Stout yield criterion [6]. This yield criterion is an extension of the generalized Hill yield criterion and has the form
The coefficients 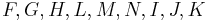 are
are
where
and 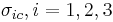 are the uniaxial yield stresses in compression in the three principal directions of anisotropy,
are the uniaxial yield stresses in compression in the three principal directions of anisotropy, 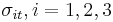 are the uniaxial yield stresses in tension, and
are the uniaxial yield stresses in tension, and 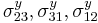 are the yield stresses in pure shear.
are the yield stresses in pure shear.
The Drucker yield criterion
The Drucker–Prager criterion should not be confused with the earlier Drucker criterion [7] which is independent of the pressure (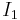 ). The Drucker yield criterion has the form
). The Drucker yield criterion has the form
where 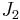 is the second invariant of the deviatoric stress,
is the second invariant of the deviatoric stress, 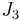 is the third invariant of the deviatoric stress,
is the third invariant of the deviatoric stress,  is a constant that lies between -27/8 and 9/4 (for the yield surface to be convex),
is a constant that lies between -27/8 and 9/4 (for the yield surface to be convex),  is a constant that varies with the value of
is a constant that varies with the value of  . For
. For 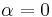 ,
, 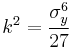 where
where 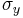 is the yield stress in uniaxial tension.
is the yield stress in uniaxial tension.
Anisotropic Drucker Criterion
An anisotropic version of the Drucker yield criterion is the Cazacu–Barlat (CZ) yield criterion [8] which has the form
where 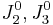 are generalized forms of the deviatoric stress and are defined as
are generalized forms of the deviatoric stress and are defined as
Cazacu–Barlat yield criterion for plane stress
For thin sheet metals, the state of stress can be approximated as plane stress. In that case the Cazacu–Barlat yield criterion reduces to its two-dimensional version with
For thin sheets of metals and alloys, the parameters of the Cazacu–Barlat yield criterion are
| Material | 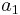 |
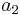 |
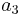 |
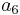 |
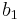 |
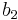 |
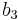 |
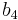 |
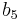 |
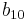 |
 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 6016-T4 Aluminum Alloy | 0.815 | 0.815 | 0.334 | 0.42 | 0.04 | -1.205 | -0.958 | 0.306 | 0.153 | -0.02 | 1.4 |
| 2090-T3 Aluminum Alloy | 1.05 | 0.823 | 0.586 | 0.96 | 1.44 | 0.061 | -1.302 | -0.281 | -0.375 | 0.445 | 1.285 |
References
- ^ Drucker, D. C. and Prager, W. (1952). Soil mechanics and plastic analysis for limit design. Quarterly of Applied Mathematics, vol. 10, no. 2, pp. 157–165.
- ^ Abrate, S. (2008). Criteria for yielding or failure of cellular materials. Journal of Sandwich Structures and Materials, vol. 10. pp. 5–51.
- ^ Gibson, L.J., Ashby, M.F., Zhang, J. and Triantafilliou, T.C. (1989). Failure surfaces for cellular materials under multi-axial loads. I. Modeling. International Journal of Mechanical Sciences, vol. 31, no. 9, pp. 635–665.
- ^ V. S. Deshpande, and Fleck, N. A. (2001). Multi-axial yield behaviour of polymer foams. Acta Materialia, vol. 49, no. 10, pp. 1859–1866.
- ^
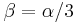 where
where  is the quantity used by Deshpande–Fleck
is the quantity used by Deshpande–Fleck - ^ Liu, C., Huang, Y., and Stout, M. G. (1997). On the asymmetric yield surface of plastically orthotropic materials: A phenomenological study. Acta Materialia, vol. 45, no. 6, pp. 2397–2406
- ^ Drucker, D. C. (1949) Relations of experiments to mathematical theories of plasticity, Journal of Applied Mechanics, vol. 16, pp. 349–357.
- ^ Cazacu, O. and Barlat, F. (2001). Generalization of Drucker's yield criterion to orthotropy. Mathematics and Mechanics of Solids, vol. 6, no. 6, pp. 613–630.
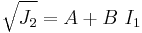
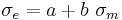
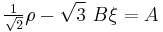
![\sqrt{\cfrac{1}{6}\left[(\sigma_1-\sigma_2)^2%2B(\sigma_2-\sigma_3)^2%2B(\sigma_3-\sigma_1)^2\right]} = A %2B B~(\sigma_1%2B\sigma_2%2B\sigma_3) ~.](/2012-wikipedia_en_all_nopic_01_2012/I/bf27d4b81a03e217c49a4fa6e08f0301.png)
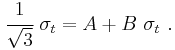
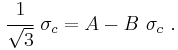
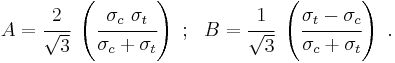
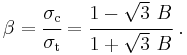
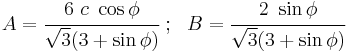
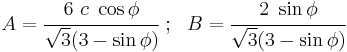
![\left[\sqrt{3}~\sin\left(\theta%2B\tfrac{\pi}{3}\right) - \sin\phi\cos\left(\theta%2B\tfrac{\pi}{3}\right)\right]\rho - \sqrt{2}\sin(\phi)\xi = \sqrt{6} c \cos\phi](/2012-wikipedia_en_all_nopic_01_2012/I/5da743ca7930578ca1f7e1c587da8869.png)
![\left[\sqrt{3}~\sin\tfrac{2\pi}{3} - \sin\phi\cos\tfrac{2\pi}{3}\right]\rho - \sqrt{2}\sin(\phi)\xi = \sqrt{6} c \cos\phi](/2012-wikipedia_en_all_nopic_01_2012/I/756be858b9a48f7f9e3d85cae4818c0e.png)
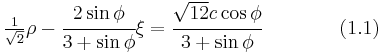
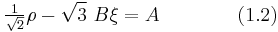
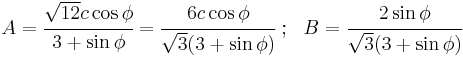
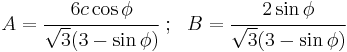
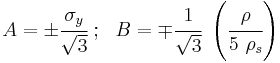
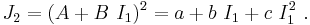
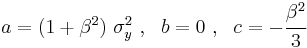
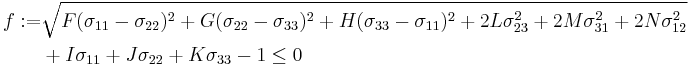
![\begin{align}
F = & \cfrac{1}{2}\left[\Sigma_2^2 %2B \Sigma_3^2 - \Sigma_1^2\right] ~;~~
G = \cfrac{1}{2}\left[\Sigma_3^2 %2B \Sigma_1^2 - \Sigma_2^2\right] ~;~~
H = \cfrac{1}{2}\left[\Sigma_1^2 %2B \Sigma_2^2 - \Sigma_3^2\right] \\
L = & \cfrac{1}{2(\sigma_{23}^y)^2} ~;~~
M = \cfrac{1}{2(\sigma_{31}^y)^2} ~;~~
N = \cfrac{1}{2(\sigma_{12}^y)^2} \\
I = & \cfrac{\sigma_{1c}-\sigma_{1t}}{2\sigma_{1c}\sigma_{1t}} ~;~~
J = \cfrac{\sigma_{2c}-\sigma_{2t}}{2\sigma_{2c}\sigma_{2t}} ~;~~
K = \cfrac{\sigma_{3c}-\sigma_{3t}}{2\sigma_{3c}\sigma_{3t}}
\end{align}](/2012-wikipedia_en_all_nopic_01_2012/I/6ba5af9d5e9001a82f70b58f5d78951f.png)
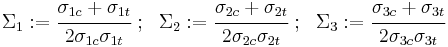
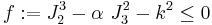
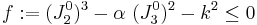
![\begin{align}
J_2^0 �:= & \cfrac{1}{6}\left[a_1(\sigma_{22}-\sigma_{33})^2%2Ba_2(\sigma_{33}-\sigma_{11})^2 %2Ba_3(\sigma_{11}-\sigma_{22})^2\right] %2B a_4\sigma_{23}^2 %2B a_5\sigma_{31}^2 %2B a_6\sigma_{12}^2 \\
J_3^0 �:= & \cfrac{1}{27}\left[(b_1%2Bb_2)\sigma_{11}^3 %2B(b_3%2Bb_4)\sigma_{22}^3 %2B \{2(b_1%2Bb_4)-(b_2%2Bb_3)\}\sigma_{33}^3\right] \\
& -\cfrac{1}{9}\left[(b_1\sigma_{22}%2Bb_2\sigma_{33})\sigma_{11}^2%2B(b_3\sigma_{33}%2Bb_4\sigma_{11})\sigma_{22}^2
%2B \{(b_1-b_2%2Bb_4)\sigma_{11}%2B(b_1-b_3%2Bb_4)\sigma_{22}\}\sigma_{33}^2\right] \\
& %2B \cfrac{2}{9}(b_1%2Bb_4)\sigma_{11}\sigma_{22}\sigma_{33} %2B 2 b_{11}\sigma_{12}\sigma_{23}\sigma_{31}\\
& - \cfrac{1}{3}\left[\{2b_9\sigma_{22}-b_8\sigma_{33}-(2b_9-b_8)\sigma_{11}\}\sigma_{31}^2%2B
\{2b_{10}\sigma_{33}-b_5\sigma_{22}-(2b_{10}-b_5)\sigma_{11}\}\sigma_{12}^2 \right.\\
& \qquad \qquad\left. \{(b_6%2Bb_7)\sigma_{11} - b_6\sigma_{22}-b_7\sigma_{33}\}\sigma_{23}^2
\right]
\end{align}](/2012-wikipedia_en_all_nopic_01_2012/I/e7d615137710d7866afbec465cda2a8f.png)
![\begin{align}
J_2^0 = & \cfrac{1}{6}\left[(a_2%2Ba_3)\sigma_{11}^2%2B(a_1%2Ba_3)\sigma_{22}^2-2a_3\sigma_1\sigma_2\right]%2B a_6\sigma_{12}^2 \\
J_3^0 = & \cfrac{1}{27}\left[(b_1%2Bb_2)\sigma_{11}^3 %2B(b_3%2Bb_4)\sigma_{22}^3 \right]
-\cfrac{1}{9}\left[b_1\sigma_{11}%2Bb_4\sigma_{22}\right]\sigma_{11}\sigma_{22}
%2B \cfrac{1}{3}\left[b_5\sigma_{22}%2B(2b_{10}-b_5)\sigma_{11}\right]\sigma_{12}^2
\end{align}](/2012-wikipedia_en_all_nopic_01_2012/I/b684c6c5e619caf86fab350cb7dd67d5.png)